ニューラルネットワークとは？をわかりやすくサクッと説明

ニューラルネットワークとは？AIを知らない人でもどこかで聞いたことあると思います。教科書的には人間の神経回路をマネすることで機械学習を実現しようというモデルです。AI？機械学習？ニューラルネットワーク？それぞれの位置づけが整理できていない方は、過去の記事↓でまとめていますので、そちらを参考にしてください。

ここでは複雑なニューラルネットワーク（多層パーセプトロン）の基本的な要素である”単純パーセプトロン”を用いて、ニューラルネットワークの中身を覗いてみようと思います。多層パーセプトロンはニューロン（データ）が複雑に絡み合っている状態を示しており、単純パーセプトロンはその一部という感じです。イメージ比較は↓。

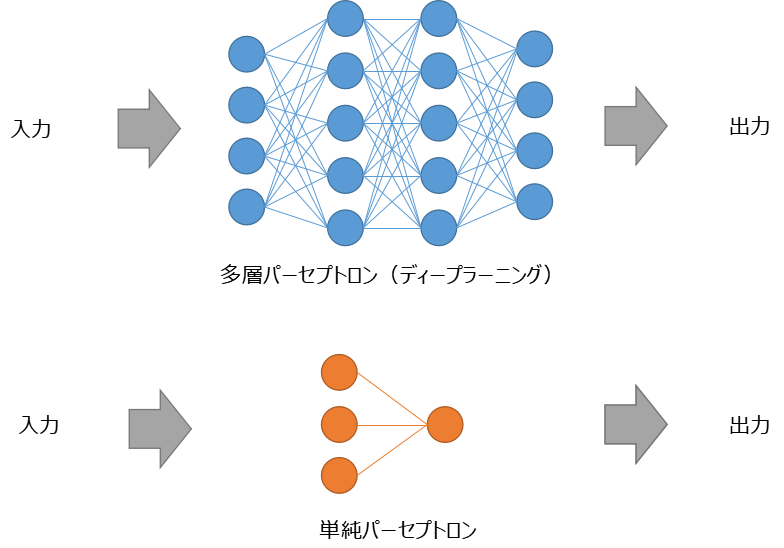
それぞれのネットワークの丸はデータを示しており、直線はデータの伝達（関係式）を示しています。例えば、多層パーセプトロンでいくと、入力データは4つで、出力データも４つ、中間に２層（隠れ層）をもつネットワークということになります。多層になると隠れ層が増えてくるので、入力と出力の因果関係が分かりにくくなってきます。ニューラルネットワークはブラックボックスと言われる所以はこの辺から来ています。

今回は、脳の仕組みを細かく説明したり、数式をたくさん使ったりはしません。ニューラルネットワークの仕組みを簡単に説明していきます。

ニューラルネットワークって響きで難しそうだよね・・・

ニューラルネットワークの中身を少し理解するだけでイメージ変わると思うよ！

こんな人におすすめ

AI・機械学習を勉強したいけど、何からやればよいか分からない
書籍が難しすぎて挫折した
これからデータサイエンティストを目指したい

ニューラルネットワークの歴史
単純パーセプトロンについて
誤差逆伝播法を少しだけ詳しく
活性化関数について
まとめ

ニューラルネットワークの歴史

ニューラルネットワークの歴史は意外と古く、現在の形になるまでに様々な”工夫”がされてきました。その”工夫”を知ることが、ニューラルネットワークの本質を理解する助けになるので、理解することをおすすめします。

ニューラルネットワークは1960年代にブーム（第1次AIブーム）を起こしたが、当時開発された単純パーセプトロンでは線形で分離できるような簡単な問題しか解けないモノでした。
1980年代になると単純パーセプトロン→多層化するであったり、誤差逆伝播法（バックプロパゲーション）を用いることにより、上記を克服できる理論が提唱される。しかし、多層化すると、勾配消失／爆発という問題が発生し、学習精度が上がらないという問題があった。
多層化による問題を解決するため、層と層の間の情報伝達を調整する活性化関数が開発され、現在のニューラルネットワークの形となる。

誤差逆伝播？　活性化関数？

超簡単に説明しましたが、ざっとこんな感じです。上のリストで謎の用語がいくつか出てきたと思います。。。これらは以下に説明していきますので安心してください。概念を理解できるとニューラルネットワークの中身がわかってきます。

単純パーセプトロンについて

まずは、ニューラルネットワークの基本的な要素である単純パーセプトロンについて、その中身を理解していきましょう！

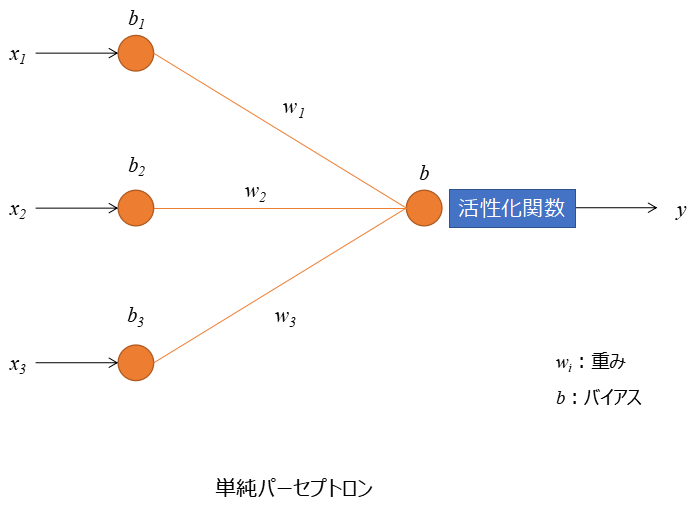
単純パーセプトロンの構成としては、入力としていくつかの情報（x1~3）を取得したとします。その入力値に重み（w1~3）、バイアス（b1~3）を調整し、活性化関数を通すことで、出力（y）を予測する。こんな感じの構成となっています。

例えば、y：傘が必要かどうか？という問題に対して、影響しそうなモノをx1：天気予報x2：季節x3：気温とします。すると↓のような式で傘が必要か？を説明できそうですよね。

傘が必要か否か＝ f {(天気予報x1 × w1 ) + (季節x2 × w2) + (気温x3 × w3) ＋ B}

これは過去の記事で説明した内容と同じですよね。以下ではこの単純パーセプトロンのイメージで説明していきます。

誤差逆伝播法を少しだけ詳しく

誤差逆伝播法とは、その名の通り誤差（予測値と実測値の差）を戻して更新していくことです。つまり、誤差が0に近くなるように重みw、バイアスbを決定して関数をつくっていくことで、イメージは前の記事でも説明した最小二乗法（誤差の二乗を最小にするw,bを取得する）と同じ感じです。

最小二乗法は変数が2つ（x, y）だったので簡単ですが、ニューラルネットワークは入力（出力）が複数あるので、問題はどうやって誤差をなくしていくかということですよね。。。誤差をなくすように更新していくアルゴリズムはいくつかあるのですが、ここでは有名な最急降下法という方法を説明します。

最急降下法

次のような縦軸が誤差、横軸に重みw1をとるグラフを考えていきます（これを損失関数と言います）。今回は簡単に説明するために誤差とw1の関係を仮に２次関数とします。

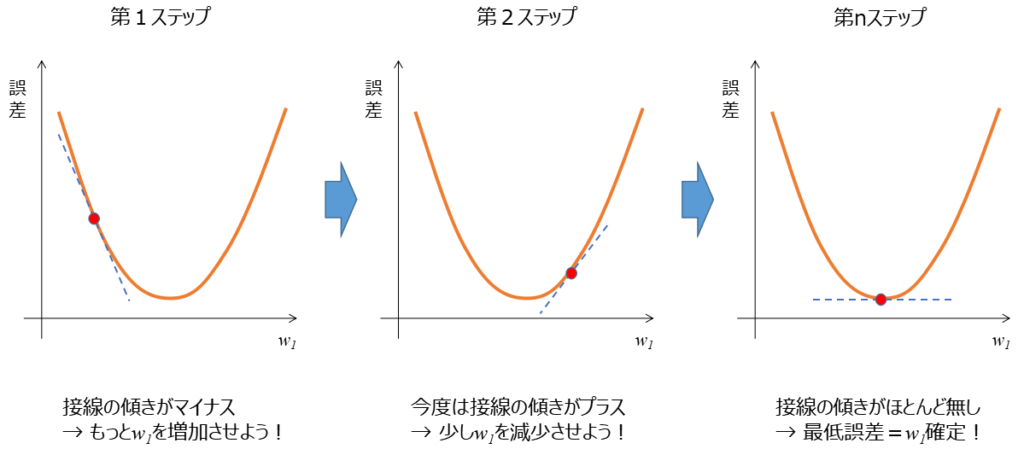
第１ステップで適当にw1を決めます。そこで接線の傾きを見てください！マイナスの傾きですよね。マイナスの場合はw1を増加させて更新します。すると次に第２ステップを見ると、傾きがプラスかつ、さっきより寝てきました。傾きがプラスなので今度はw1を減少させよう。…っとこんな感じで更新していき、最終的には第nステップで傾きがほぼ０となり、誤差が最小となることでw1を確定させる。これが最急降下法です。

こんな感じの繰返し計算をひたすら実行していくことで重みw1~3、バイアスb1~3をどんどん更新していきます。これが誤差逆伝播法です。更新していくときに合成関数の微分である連鎖律を利用しているのですが詳細は割愛します。イメージとしては、更新していく中間層でいろいろ計算するのですが、結局のところ入力データxから出力データyを説明するため↓の様な微分式を利用しているという感じです。どんな複雑な関数でも1個1個が微分可能なら、その合成dy/dxは微分できるという考え方です。

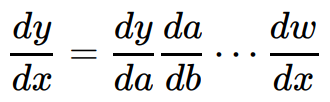
上でも軽く触れましたが、誤差逆伝播法は最小二乗法とイメージ近いです。概念の理解としては、単純パーセプトロンの図へ戻って説明すると、オレンジの丸はデータ、オレンジの直線は最小二乗法、それらを加算しyを説明していくことになります。加算したものを最後に活性化関数というフィルターに通すのですが、次にそれを説明します。

最小二乗法の詳細は↓を見てください。

活性化関数について

活性化関数はある一定以上の値であればデータを出力するが、一定以下であればデータを出力しないような関数です。例えば、〇×の判定であれば、データが出力されれば〇、出力されなければ×といった感じです。活性化関数を導入することで、非線形的な（人間っぽい？）変換が可能となり、モデルの表現力を向上させることができます。

活性化関数はどのような出力の形態にしたいか？で様々な提案がされています。正解はこれ！というモノは無いですが、代表的なモノを載せておきます。

シグモイド関数　…　２クラス分類（〇×判定など）のモデルで用いる
ソフトマックス関数　…　多クラス分類（犬、猫、車、人など）のモデルに用いる
ReLU関数　…　ニューラルネットワークの中間層（隠れ層）でよく用いる人気の関数
ステップ関数　…　単純パーセプトロンで用いる
恒等関数　…　回帰モデルで用いる
tanh関数　…　シグモイド関数の進化版

〇×判断をしたいときはすべてシグモイド関数を使っておけばOKってこと？

注意点として、ディープラーニング（多層パーセプトロン）モデルをつくるとき、中間層にシグモイド関数を乱立させると勾配消失という現象が発生します。勾配消失とは、文字通り勾配が消えることで、上で説明した最急降下法でwの値が更新されなくなることを言います。

少し難しい説明をすると、シグモイド関数の微分最大値が0.25であるため、各層の出口で0.25以下の数値を掛け算していくことになります。そのため2層目以降で勾配がほとんどなくなってしまう勾配消失が発生するのです。それを改善させようとtanh関数（微分の最大値：1）や、ReLU関数（入力が正だと微分値は常に１）が開発されてきました。