正規分布について

著者がポイントとして考える、AIの基礎をできるだけ簡単な形でお伝えします。書籍等で勉強する前にご一読いただけると、理解を深めることができると思います！

AI・機械学習は確率分布という概念で成立しています。というのも何かを予測するときに、ある結果が起こりやすいと分かっていると予測の精度は当然大きく向上しますよね。確率分布はある結果の起こりやすさの分布です。

確率分布には様々ありますが、最も有名なモノのが正規分布です。ガウス分布とも言います。ここでは正規分布について紹介していきます。正規分布は自然界のあらゆるところで、何故か？この分布に従ってしまうという魔法のような分布です。迷ったときに使えるので是非最後まで読んでみてください！

正規分布（ガウス分布）とは

正規分布とはどのような分布か？これは難しい数式ありますが。ここでは図で理解しましょう。数式を知りたい方は正規分布の確率密度関数を調べてみてください。

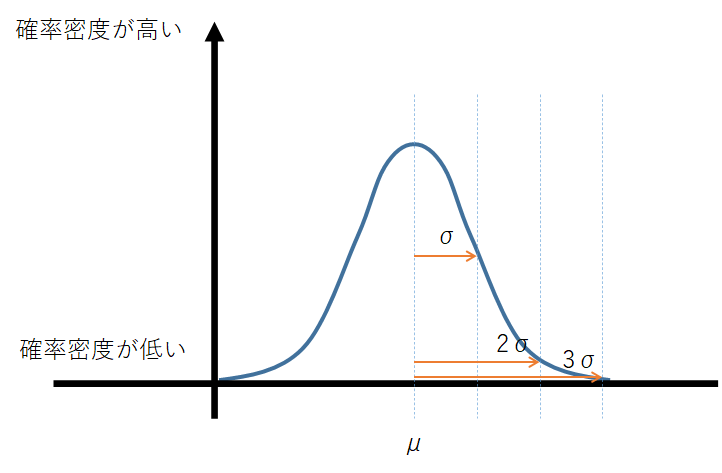
正規分布はこんな感じの「ひと山型」、「左右対称」のベル型分布です。ここで、μは母平均（神のみぞ知る真の平均値）、σは標準偏差を表しています。統計学の豆知識として、ギリシャ文字で定義されるモノは基本的に神のみぞ知る値です。起こりえる全部の値を調べて平均値を出すなんて不可能ですよね。だからμと置くのですが、実際はランダムサンプリングした平均値≒μと考えていきます。標準偏差も一緒。

さて、正規分布は山の一番高いところのx軸は母平均（μ）であり、この分布の面積は確率を示しています。例えば、標準偏差の2倍＝2σが母平均μからバラツくμ＋2σを考えます。このμ＋2σが起こる確率は下図で示すように5%となります。

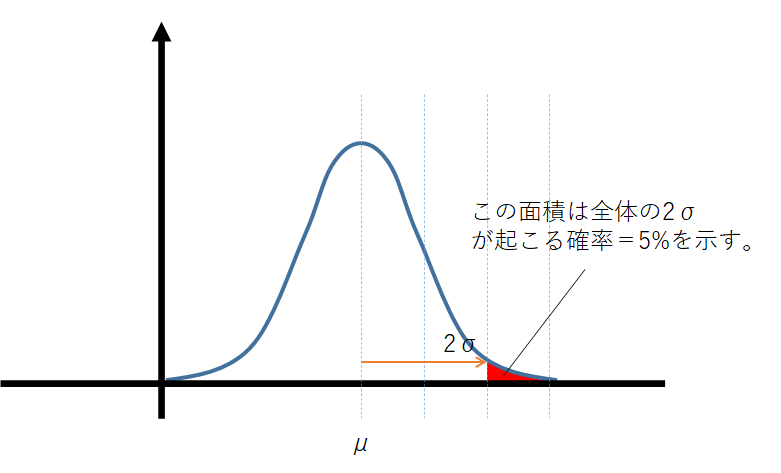
これは何ぞやと言うと、例えば、饅頭の大きさとかで考えてみると、平均的な饅頭の大きさはμ＝100g、標準偏差（バラツキ）σ＝5gとしたら、

$$ 饅頭の大きさ = 100g + 2 * σ = 110g $$

110ｇの饅頭が5%の確率で存在するということです！おばちゃんのバラツキが大きくσ＝10ｇとなればなんと120gの饅頭が5%の確率で存在するということになります。

まとめますと、

ということになります。便利ですね。ちなみに、

• σ : 68%
• 2σ : 95%
• 3σ : 99.7%

という数字を覚えておくと更に便利です。正規分布に従えば、饅頭の大きさがμ＋σ以内に収まる確率が68％、μ＋2σ以内が95％、μ＋3σ以内が99.7％ということになります。ということは、3σ以内にほとんどが収まるので、製造業では±3σを管理範囲にすることもあります。

大数の法則、中心極限定理とは

正規分布に従えば便利な計算が可能になることは分かったと思いますが、実際に正規分布に従うのか？という疑問がると思います。

大数の法則とは、サンプル数を増やしていくと、その平均値は母平均μへ近づいていくという法則です。これは何となくわかると思います。

中心極限定理とは、どんな確率分布であってもサンプル数を増していくと、その平均値の分布は正規分布に近づいていくという法則のことです。

これらのことを例えばサイコロの目で考えると、サイコロを振って出た目をプロットしても正規分布にはなりませんよね。しかし、100回振って出た目の平均値をプロット→100回振って出た目の平均値をプロット・・・・これを繰り返しプロットしていくと、平均は大数の法則より3.5となり、中心極限定理より正規分布になるということです。

つまり、次に出る目を予測することは非常に難しいけれども、100回振った平均を予測するのはできそう！ということです。感覚的にもそうですよね。

不思議ですよね。この法則のおかげで多くの場合は正規分布として近似する考えが成立します。正規分布として近似することができるということは、既に勝ち申したということで、↑で書いたようにその空間で起こりえることを掌握しているということになります。

まとめ

正規分布の考え方を説明しましたが、難しかったと思います。私も最初に勉強したときは理解できませんでした。しかし、正規分布は統計学という学問の根源なので、検定・推定、分散分析、実験計画法などあらゆるところで活用されています。そこでよく分からなくなったときに、戻ってきて学習するのが私には効果的でした。具体的な使い方もわかるので。ご参考に！！