【説明可能なAI】「解釈可能な機械学習」を読んで感じたこと

企業でAIを導入しようとするとき、まず立ちはだかる壁はAIに精通していない人（主に上司？）へ有効性を説明することです。これについては、私自身答えはなく難しい問題と思っています。特にディープラーニングは厄介で、つくった本人が何故そうなるか？説明できない…なんてことも良くあることだと思います。

データサイエンティストであるクリストフ・モルナル氏による著書『Interpretable Machine Learning──A Guide for Making Black Box Models Explainable／解釈可能な機械学習──ブラックボックス化したモデルを説明可能にするためのガイド』の日本語訳がWeb上で無料公開されています。この本にディープラーニングを説明するヒントが記載されています。

AIを説明可能にするためには２つの手法があります。線形回帰、決定木など、「本質的」に解釈可能なモデルをつかうか、ディープラーニングなどのブラックボックスの結果を使って「後付け」で解釈していくかです。

ここでは、ディープラーニングを説明することが可能な「後付け」解釈である”モデル非依存な手法”について、内容を少しまとめておきます。文章だけだとわかりにくい（わからない）と思います。興味ある方は原文を読んでいただくとグラフ付きで分かりやすいと思います。

モデル非依存(Model-Agnostic)な手法をまとめる
モデル非依存(Model-Agnostic)な手法の一例
まとめと感想

モデル非依存(Model-Agnostic)な手法をまとめる

5章の序盤にあるこの絵が、モデル非依存な手法を物語っていると思います。

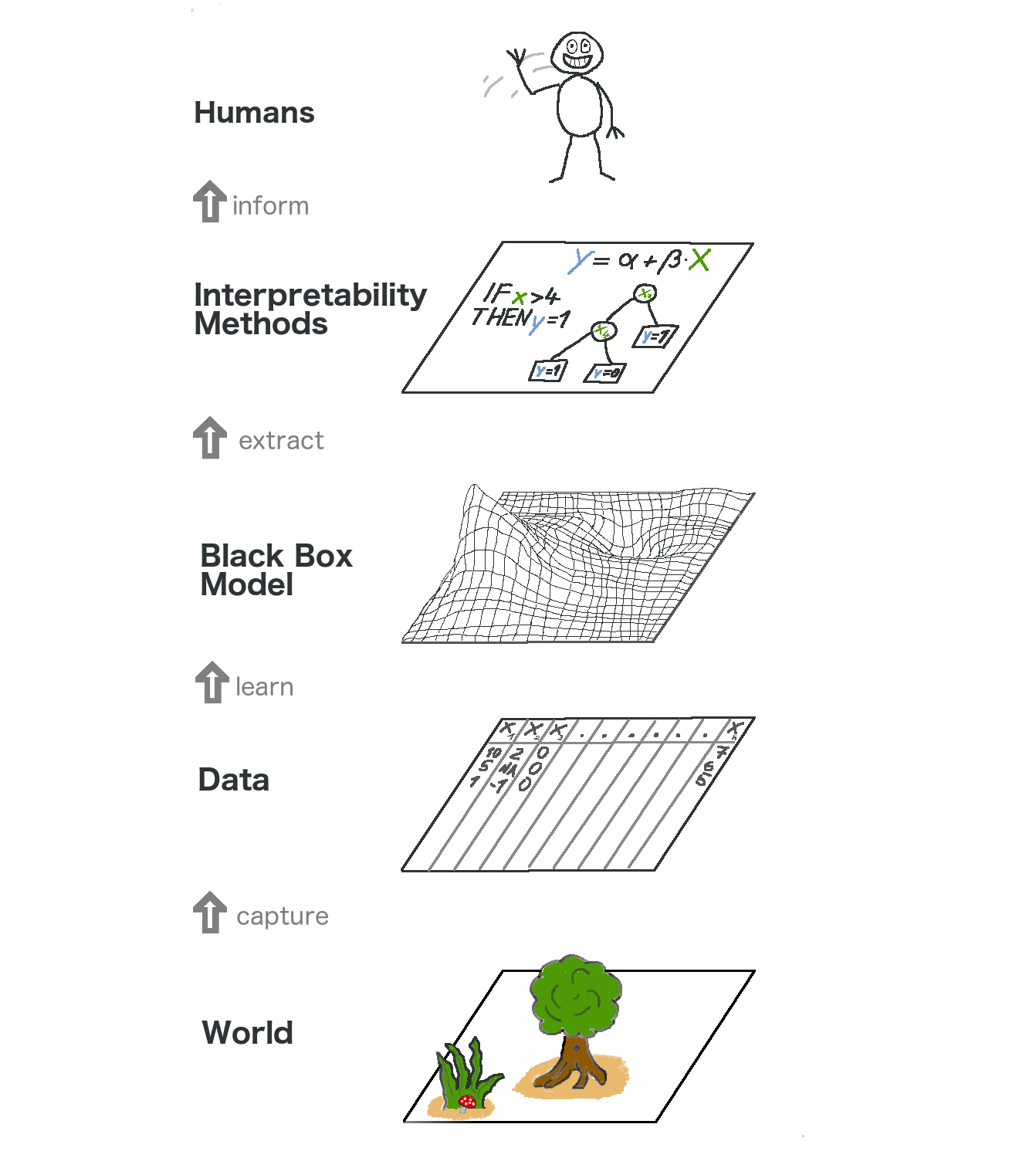
説明可能な機械学習の全体像。説明が人間に届く前に、現実世界はいくつかの層を通過します。 — 出典：Interpretable Machine Learning
https://hacarus.github.io/interpretable-ml-book-ja/agnostic.html

一番下の層が現実世界で、二番目はデータ層です。データ層では現実世界をデジタル変換したものです。下から三番目の層が機械学習の層でブラックボックスとなります。その上の四番目の層に解釈手法の層があります。最後に人間の層がある。これが説明可能な機械学習の全体像。説明が人間に届く前に、現実世界はいくつかの層を通過します。

ここで、統計的な判断をする統計学者の振る舞いを考えると、ブラックボックスモデルの層を飛ばし、直接解釈手法の層へと進み、解釈を人間へ伝えます。一方で、機械学習のスペシャリストはブラックボックスな機械学習モデルを学習させます。解釈手法の層は飛ばされ、直接ブラックボックスモデルを人間へ伝えます。

機械学習モデルを解釈可能とすることは統計学者と機械学習のスペシャリストの考えを融合させることで成立します。なので非常に難しい分野の研究となっているんですね。。。

モデル非依存(Model-Agnostic)な手法の一例

以下は、私の備忘録として書き残しているため、理解が難しい場合は飛ばしてしまっても大丈夫です。この辺は使える考え方だと思いました。

５．１　Partial Dependence Plot（PDP）・・・2つの特徴量に限定し、関係性を抽出することで関係性を見える化する。つまり、縦軸に目的変数／横軸に説明変数をとるグラフを表示することです。長所：因果関係の説明が分かりやすいこと。短所：①最大の特徴量の数が２つであること。３次元以上になると我々がうまく想像できません。②特徴量間での独立性が仮定されていること。特徴量間で相関があると説明できなくなります。これは重回帰分析で言う多重共線性のことです。③PDPは平均的な周辺効果のみを示すので不均一な影響が隠れてしまう可能性がある。（詳細は5.1)

５．２　Individual Conditional Expectation（ICE）・・・PDPの短所③不均一な影響が隠れてしまう可能性を回避するため、個々のインスタンスに対してPDPを実施する手法です。長所：直感的に理解可能。不均一な関係性を明らかにできる。短所：①1つの特徴量のみしか理解が難しい。②線の中のいくつかの点は妥当でないデータ点となる可能性がある。いわゆる外れ値みたいなモノが混在し理解を惑わす可能性がある。③プロット線が重なり合い見ずらい。

５．３　Accumulated Local Effects (ALE) Plot・・・PDPにおいては外挿予測による精度の影響を受けることで目的変数との関係性にノイズが入る可能性があるが、ALEは平均値との差分（誤差）をとることで外挿予測のノイズを打ち消すことができPDPより高い信頼性がある。長所：①ALEは特徴量が相関しているときでも機能する。②PDPよりも計算が高速。③平均値との差のため0に中心化される。短所：平均をとる区間数が多いときに、値が不安定（ばらつく）ことがある。

５．５　Permutation Feature Importance・・・特徴量を並び替えたあとのモデルの予測誤差の影響を比率で計算する手法で、特徴量の重要度を計算する。徴量の値を入れ替えるとモデル誤差が増加する場合、モデルは特徴量に依存した予測をしているので、その特徴量は「重要」。特徴量の値を入れ替えてもモデル誤差が変わらない場合、特徴量は「重要ではない」と言える。長所：①特徴量重要度の測定値が異なる問題間で比較可能。②相互作用があっても解釈可能。③モデルの再学習は不要。短所：①特徴量の重要度を計算するときに学習データを用いるべきか、テストデータを用いるべきか明確でない。②相関した特徴量があると両方の特徴量の間で重要度を分割することで、関連する特徴量の重要度が低下する。

５．６　グローバルサロゲート (Global Surrogate)・・・このモデルは他とは一風変わっており、ディープラーニングなどブラックボックス手法でつくったモデルの予測値を取得する。その予測値と、元のデータセットを使って解釈可能なモデル（線形回帰、決定木など）を用いたサロゲートモデル（代替えモデル）をつくる。サロゲートモデルをモデルを解釈することで元のデータを説明する手法。長所：様々なモデルが使える柔軟性をもつ。R2スコアで解釈できるので直感的。短所：サロゲートモデルの解釈はデータではなくモデルについての結論である。