著者がポイントとして考える、AIの基礎をできるだけ簡単な形でお伝えします。どちらかというとデータサイエンティストの方へというよりは、現場実務者であったり、文系出身の方向けの内容となっております。書籍等で勉強する前にご一読いただけると、理解を深めることができると思います!
回帰分析という言葉でよくわからない人でも、相関関係とか、近似直線を引くとか言うとイメージしやすいかと思います。例えば、身長と体重の関係、アイスクリームの販売数と気温などは、何か関係がありそうですよね。ここでは、そのような関係性を明らかにして、次に得られる値を予測する方法を説明していきます。
- 回帰分析について
- 回帰モデルの評価
- AI・機械学習を勉強したいけど、統計学がよく分からない
- 書籍が難しすぎて挫折した
- これからデータサイエンティストを目指したい
AI・機械学習において回帰分析は根底となる理論です。これをある程度理解しているのと、そうでないのではAIの性能に大きく差がつく大切な理論です。
また、回帰分析を診断することでAIが人と同じような回答を出せているか?誤差のバラツキを見ることでAIの表現力を評価することが可能です。
更に、回帰分析を診断し誤差の分布を見ることで、AIにもう少しデータを学習させた方が良くなるかも?なんてこともわかったりします。
ここでは回帰分析について、できる限り易しく説明していきます。最後まで読んでいただけると、おそらく統計的な物の見方・考え方がぼんやり見えてくると思います。難しい理論は理解できなくても、我慢して最後まで読んでいただくことをおすすめします!
たぶん、長いので2回に分けます…
回帰分析について
ここで、回帰分析の中で最も単純な単回帰分析を例に説明していきます。単回帰分析?全くきいたことなくて吐き気がするんですが…という方、安心してください!
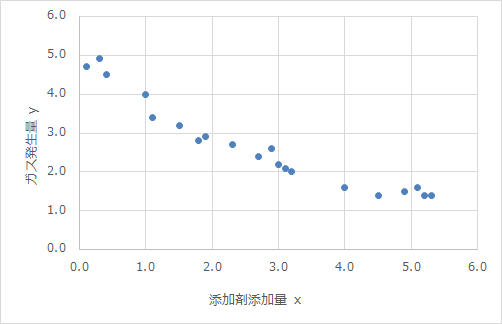
こんな感じのやつです。多分皆さん見たことありますよね。目的変数(y)を一つの説明変数(x)で表すので、単回帰と呼ばれています。
では、このグラフからどんなことが読み取れるでしょうか。

相関関係でしょ!それくらいはわかりますよ!
そうですね!xとyがどんな関係にあるか、その相関関係が分かりますよね。では、グラフにエクセルの近似直線を引いてみます。
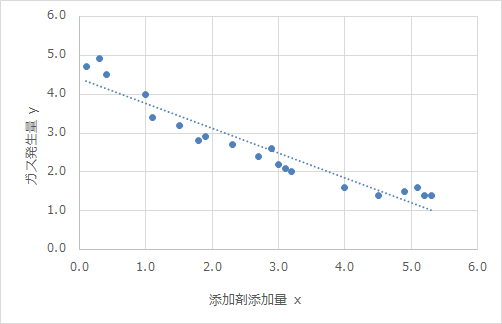
このグラフからは何が読み取れますか?

直線上にデータが乗るってことかなぁ?
そんな感じですよね。近似線を引くことで、x、yの関係がさらによくわかり、取得していない場所のデータも予測することができますよね。この線を引くことが回帰分析です!
では、この近似線はどういうルールで引かれているのでしょうか?

え!ルールなんてあったの?エクセルの機能かと…
この近似直線は「最小二乗法」というルールに従って引かれているんです。
最小二乗法について
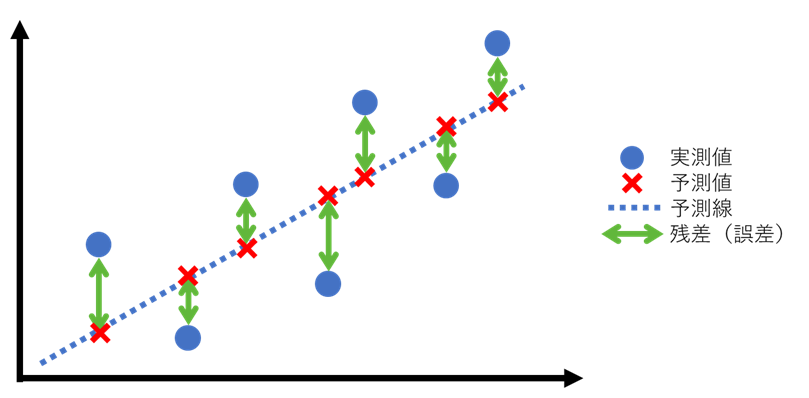
図で説明すると、実測値と予測値の差である残差が一番小さくなるように予測線を引くことが最小二乗法です。つまり、緑の矢印の長さを最小にするということです。
最小二乗法の二乗はどこから来たのかというと、予測値ー実測値を計算すると、+(正)と-(負)の両方が出てきちゃいますよね。めんどくさいので二乗して負の符号を消してしまうだけです。ちょっとだけ式で説明するとこんな感じです。
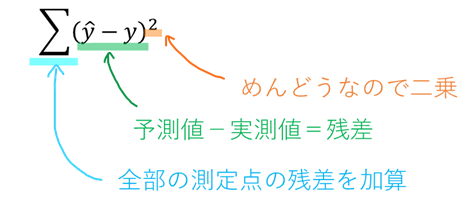
上の式で算出される数値が最小になるように予測線をとってあげるのが、最小二乗法になります!つまり、各測定点における残差のバラツキが最小になるように設定されております。この考え方はニューラルネットワークでも同じなので覚えておくと良いです。
回帰モデルの評価
最小二乗法でつくった回帰式(ここでは回帰モデルと呼びます)が、どのくらい良いものなのか?を評価することができます。
- 決定係数について
超重要な指標の一つに決定係数があります。決定係数は説明変数(x)が目的変数(y)の値を説明(決定)しているかの指標です。どういうことか、イメージで理解しておきましょう!
身長(x)と体重(y)のデータがあったとします。予測値と実測値で差(残差)があり、残差は測定点毎に違うのでバラツキがあることを説明しました。ここで、そのバラツキを下図のように表してみます。

体重のバラツキをSyと表現するとSyの中には、当然デブとガリがいるので、身長で体重を説明できないバラツキSxyが存在します。身長のバラツキを体重のバラツキのみで説明しようとすると右図のような穴あきとなり、Sy-Sxyで説明できると思います。決定係数は純粋な体重のバラツキと、身長のバラツキで説明できる体重のバラツキの割合で算出される係数となります。
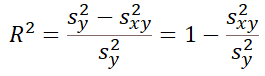
ここで、R2は決定係数と呼ばれています。決定係数R2が1に近ければ、説明力が高いということになり、精度の高い予測がおこなえていることを表します!
決定係数は説明力を表す指標で、1に近ければ高い精度の予測モデルと評価することができる
根拠はよくわかりませんが決定係数0.8以上が良いと言われています。
- RMSE (Root Mean Squared Error) について
もう1つよく使う評価手法としてRMSEがあります。RMSEは実は既に半分くらい説明している理論になります。式で説明します。

最小二乗法で出てきた残差のバラツキをn(測定点数)で割って、次元を戻すためルートしただけです。つまりは、残差のバラツキを標準化して他と比べ易くしているだけなんですね!
RMESは、残差のバラツキを標準的な数値化し比較できるようにする
他にもルートを使わないMAEという評価手法もありますので、気になる人は調べてみてください。
ここはかなり大事なことで、この先の理論(ニューラルネットワークとか)でも使っていきますので、何度も読み直して感覚を掴んでもらえればと思います。
パート1まとめ
- 回帰分析は説明変数と目的変数の関係から、目的変数を予測すること!
- 最小二乗法によって残差のバラツキが最小になるような回帰モデルをつくることができる!
- 決定係数は回帰モデルの説明力を表す指標!1に近ければ高い精度と評価できる
- RMESは、残差のバラツキを表す指標!
パート2では、他であまり紹介されていない手法をご紹介します。特にビックデータを取得できない人や、スパースデータを使いこなしたい人にはおすすめな内容になると思います!



コメント