著者がポイントとして考える、AIの基礎をできるだけ簡単な形でお伝えします。書籍等で勉強する前にご一読いただけると、理解を深めることができると思います!
回帰分析パート②始めます。パート①では回帰分析の基礎、評価方法を説明しました。詳しくは↓
- 残差のバラツキからAIの表現力を見る
- 残差の分布からAIに質の良いデータが与えられているかを見る
- 機械学習モデルの精度がでない
- 書籍が難しすぎて挫折した
- これからデータサイエンティストを目指したい
ここでは、つくった回帰モデルを診断することでAIが人と同じような回答を出せているか?残差(誤差)のバラツキを見ることでAIの表現力を見たり、次のアクションを考察する(例えばAIにもう少しデータを学習させた方が良くなるなど)方法を説明します。
回帰診断とは
回帰診断とは、つくった回帰モデルが未知のデータに対し性能を発揮できるかどうか、診断する方法です。いくつか提案されていますが、私が使ってみて効果あると実感したものをご紹介します。
残差のヒストグラムを使え!
いきなり訳が分からないタイトルだと思いますが、順を追って説明していきますので聞いてください。
ヒストグラムは↓で詳しく説明しているので不安な方はご一読ください。
回帰分析パート①で最小二乗法による回帰モデルをつくったと思います。実は回帰モデルはいくつかの仮定の基で成立しています。
- 残差の不偏性
- 残差の等分散性
- 残差の独立性
- 残差の正規性

???ちょっとまて…
ですよね。グラフで少し説明します。
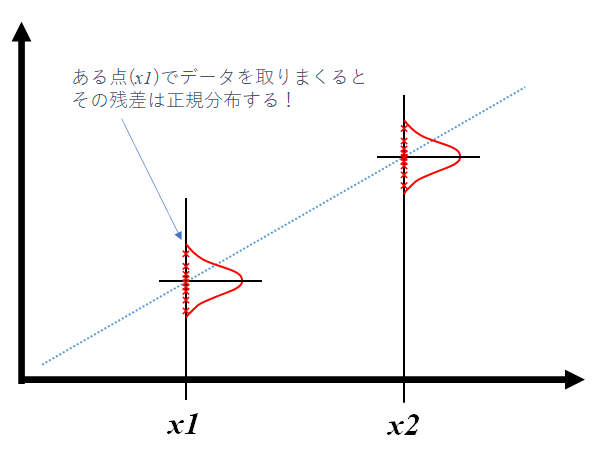
回帰モデルのある点(x1)でデータを取りまくってください。実データは様々な要因によってバラツキますよね。このバラツキをグラフ化するとなんとなく赤線のグラフとなるのは感覚的にわかりますよね。この赤線のグラフが残差のヒストグラムです。
残差が不偏性(グラフの中心線が回帰線と交わる)、等分散性(x1でもx2でも同じ赤線のグラフ)、独立性(残差間の相関なし)、正規性(正規分布する)となることを前提として、回帰モデルは精度が出るように設計されています。→つまり残差のヒストグラムがキレイな正規分布であればOKということです!
ということは、つくった回帰モデルの残差を分析することで精度を診断することができるということです。

分かったような、分からないような。とにかく残差をグラフ化せよってことか?
そうですね。実例でやってみましょう!感覚がつかめると思います。
回帰診断の実例
下図のような回帰モデルがあるとします。
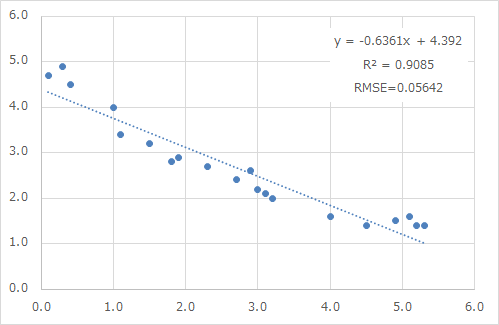
この回帰モデルは決定係数R2=0.9085とよく相関関係を説明しており、RMSE=0.05642でバラツキも非常に小さいため、良い回帰モデルと判断することができます。

かなり良い回帰モデルですよね。これ以上ないでしょ!
ちょっとまってください!実はさらに精度を上げることが可能です!とにかく、残差のヒストグラムを見てみましょう。
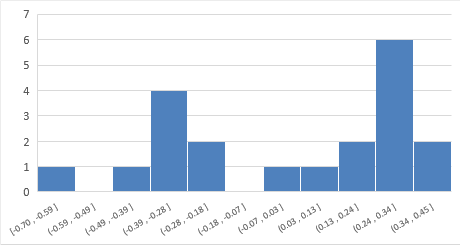

あれ、正規分布じゃないぞ…
データ数が少ないので、はっきりとしたことが言えないのですが、これは正規分布ではないですよね…。このような場合、この回帰モデルで予測していくと結果がズレる確率は上がります。
上図のように2つの山ができているときは次のことが考えられます。
- 線形(直線)の回帰モデルに当てはまっていない
- 2つの要因が目的変数(y)へ影響している
ここまでのことが分かってしまうのです!!
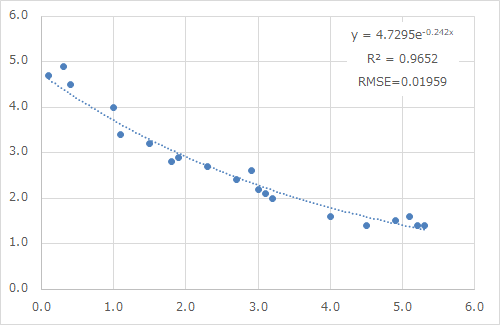
ちょっと回帰モデルを修正してみましょう。回帰モデルを線形→非線形へ変えてみます。
| R2 | RMSE | |
| 線形回帰モデル | 0.9085 | 0.0564 |
| 非線形回帰モデル | 0.9652 | 0.0195 |

ホントに性能が良くなった!
このように回帰診断をすることで、簡単に性能を上げることができます。ちなみに機械学習のデータの前処理は回帰診断のような統計的な見方をする作業が非常に大切となります。データサイエンティストの仕事8割が前処理と言われているのは、こう言ったデータの本質を1つずつ見抜いて処理していく必要があるからですね。
ここまで説明してきてどうでしょうか、ぼんやりと統計的な見方が分かってきたんじゃないでしょうか?ポイントはバラツキです。統計的な見方とはバラツキ(分布)を見るということで、個々のデータはあまり気にしないで良いのです。
一方で、研究者や開発担当の方々は個々のデータにこだわります(私の周りもそうです)。そういった中で、上記のような統計的なモノの見方で一石を投じると失敗がグッと減るのが、私の実感です!
まとめ
- 回帰モデルの残差の分布を分析することでモデルの表現力を診断することができる。
- 残差ヒストグラムの形状から、データの不足や回帰モデルの当てはまりなどが分かる。
- 統計的なモノの見方は、バラツキ(分布)を見るということ。
最後に、統計的なモノの見方は一日でどうにかなるようなモノではありません。1回読んだだけではなかなか難しいと思います。何度も読んで、感覚を掴んでいってください。




コメント